|
مثال
:
معياري انحراف جي قيمت معلوم ڪرڻ جڏهن ته انحراف
ڪنهن فرضي برابري واري عدد مان ورتل هجي.
Deviation
=
d
|
انحراف 2 ڪثرت
f2 d2 |
انحراف ڪثرت
F
x d |
انحراف برابر عدد
d |
ڪثرت
f |
وچون عدد
Mid Point |
ڳڻپ
Score |
|
64
-
36
50
32 |
8
-
6
10
8 |
8
7
6
5
4 |
1
0
1
2
2 |
132
127
122
117
112 |
134-130
129-125
124-120
119-115
114-110 |
|
انحراف 2 ڪثرت
f2 d2 |
انحراف ڪثرت
F
x d |
انحراف برابر عدد
d |
ڪثرت
f |
وچون عدد
Mid Point |
ڳڻپ
Score |
|
18
12
3
-
11
12
36
32 |
6
6
3
-
11-
6-
12-
8- |
3
2
1
0
1-
2-
3-
4- |
2
3
3
4
11
3
4
2 |
107
102
97
92
87
82
77
72 |
109-105
104-100
99-95
94-90
89-88
84-80
79-75
74-70 |
|
306 |
10 |
|
38 |
|
|
نموني طور ورتل مواد جا قسم:
KINDS OF SAMPLING
DATA
نموني طور ورتل مواد جا ٻه قسم آهن:
(1)
ابتدائي مواد Primary
Data
(2)
ثانوي مواد Secondary
Data
انگن
اکرن ۾ ابتدائي مواد انهيءَ کي چيو ويندو آهي،
جيڪو پهريائين اڻ ترتيب ڏنل حالت ۾ گڏ ڪيو وڃي ۽
ثانوي مواد انهيءَ کي چيو وڃي ٿو، جيڪو گهٽ ۾ گهٽ
هڪ دفعو انگن اکرن واري ترتيب تي رکيو ويو هجي، يا
ائين چئجي ته ابتدائي مواد معنيٰ اهو مواد جيڪو
جيئن ۽ جهڙي انداز ۾ مواد گڏ ڪيو ويو هجي، پر
انهيءَ کي ڪنهن ترتيب تي رکيو ويو هجي ته انهيءَ
کي ثانوي مواد چيو وڃي ٿو. معنيٰ ابتدائي مواد کي
جيستائين ڪنهن ترتيب تي نٿو رکيو وڃي اوستائين اهو
ابتدائي مواد آهي، پر جڏهن انهيءَ کي ترتيب وار يا
فهرستن گرافن ۽ نقشن ۾ ڏيکاريو وڃي ٿو، تڏهن
انهيءَ جي حيثيت ثانوي مواد جي ٿيو وڃي.
ڪم
ايندڙ مواد جي چونڊ:
Selection of
Representative
Data
جڏهن
ڪابه تحقيق دائري جي لحاظ کان تمام وڏي هجي ۽ عملي
طور انهيءَ کي مڪمل ڪرڻ مشڪل هجي ته اهڙي حالت ۾
تحقيق هيٺ ايندڙ شين يا حالتن ۾ اهڙيون شيون يا
حالتون چونڊيون وڃن. جيڪي پوري تحقيق جي نتيجي
لاءِ نمائندگي ڪنديون هجن تن کي انگن اکرن جي
اطلاع موجب نموني طور ورتل مواد (Sample
Survey)
چيو ويندو آهي، جيڪو پوري تحقيقي ائري نمائندگي
ڪندو آهي. اهڙي طرح ٻن طريقن تي مواد جا نمونا
چونڊيا ويندا آهن:
(1)
خصوصي چونڊيل نمونا
Deliberate or
Purposive Selection
(2)
عام کنيل مواد
Random or
Sampling or Chance Selection
خصوصي چونڊيل مواد:
Purposive
Selection
نموني طور : Sampling
جڏهن
ڪنهن تحقيق ۾ يا گهربل معلومات لاءِ وقت گهٽ هوندو
آهي ۽ مواد گهڻو يا تحقيق جو دائرو وڏو هوندو آهي،
تڏهن ٿوري وقت ۾ گهٽ خرچ سان جلدي ۾ نتيجو ڪڍڻ
لاءِ پوري مواد مان ڪي نموني طور مثال ورتا ويندا
آهن، جن کي پوري مواد لاءِ نمائندو تصور ڪيو ويندو
آهي ۽ انهيءَ نموني طور ورتل مثالن مان ورتل مواد
جو تجزبو ڪري ۽ نتيجو ڪڍيو ويندو آهي. انهيءَ لاءِ
ضروري هوندو آهي، ته جيڪو نموني طور مواد ورتو وڃي
اهو ايترو ننڍي انداز ۾ يا ٿورو نه هجي جو غلط
نتيجو نڪري اچي پر ايترو مواد هجي، جنهن مان نتيجي
ڪڍڻ ۾ مدد ملي سگهي.
سمجهو ته ڪنهن ملڪ ۾ ماڻهن جي اقتصادي حالت کي
ڏسڻو آهي پر جيئن ته پوري ملڪ جي ماڻهن جي اقتصادي
حالتن معلوم ڪرڻ لاءِ وقت، محنت ۽ پئسي جي ضرورت
هوندي آهي تنهن ڪري انهن ٽنهي ڳالهين کي نظر ۾
رکندي يا انهن ٽنهي جي ڪمي جي ڪري پوري ملڪ مان ڪن
خاص شهرن يا ڳوٺن کي، جن کي ضروري سمجهيو ويندو
آهي يا جن کي نمائندگي جي لاءِ ضروري سمجهيو ويندو
آهي. تن کي تحقيق لاءِ چونڊيو ويندو آهي. انهيءَ
لاءِ هڪ ڳالهه جو خيال رکڻ گهرجي ته تحقيق ڪندڙ
کي اهڙي تحقيق ۾ پنهنجي پسند جا نمونا نه چونڊڻ
گهرجن، پر اهڙا نمونا چونڊڻ گهرجن جيڪي پوري
تحقيقي دائري جي نمائندگي ڪن. جيڪڏهن ائين نه
ڪيائين ته ٿي سگهي ٿو ته نتيجو صحيح نه اچي سگهي.
عام
کنيل نمونا:
Random
Sampling
عام
کنيل نمونن ۾ تحقيق ڪندڙ جو شخصي لڳاءُ نه هوندو
آهي. هن ۾ تحقيق ڪندڙ کي جيڪي نمونا اڳيان هوندا
آهن، انهن تي تحقيق ڪندو آهي. هن جو طريقو هيءُ
هوندو آهي ته سمجهو ته ڪنهن ملڪ جي اقتصادي حالتن
تي تحقيق ڪرڻي آهي، انهيءَ لاءِ سڀني شهرن ۽ ڳوٺن
جي لسٽ تيار ڪئي ويندي آهي ۽ انهن مان ڪنهن مقرر
نمبرن تي ايندڙ شهرن يا ڳوٺن کي چونڊيو ويندو آهي،
جن تي تحقيق ڪئي ويندي آهي. سمجهو ته هر پنجن
نمبرن کان پوءِ ايندڙ شهر کي چونڊڻو آهي. اهڙي طرح
سڄي لسٽ مان پنجين پنجين نمبر تي ايندڙ شهرن يا
ڳوٺن کي چونڊيو ويندو آهي.
تخمينو لڳائڻ :
Making
Inference
هن
کان اڳي انگن اکرن بابت رڳو بياني مقصد
Descriptive Function
کي
ظاهر ڪيو ويو آهي. انهيءَ کان سواءِ انگن اکرن جي
مدد سان ڪنهن شيءِ يا ڳالهه بابت تخمينو لڳائي
سگهجي ٿو ۽ انگ اکر اهڙي نتيجي لاءِ تمام صحيح
طريقو آهي. هن طريقي ۾ هر شيءِ جا نمونا
Samples
ورتا ويندا آهن ۽ انهن جي مدد سان نتيجو ڪڍيو
ويندو آهي. سائنسي تحقيق جا سڀ اصول انهن تي ٻڌل
آهن. ليڪن هن طريقي سان ڪيترن حالتن ۾ نتيجو ڪڍڻ
ناممڪن هوندو آهي ڇو ته سائنسي قانون محدود مشاهدي
جي اندر ڪم ڪن ٿا ۽ هر ڪنهن تخميني لڳائڻ لاءِ
ائين چئي سگهجي ٿو ته جيڪڏهن حالتون ساڳيون رهيون
ته (جنهن جو اصطلاحي مطلب آهي ته
Probability Occurance
(امڪان وقوع پذير) ته نتيجو ساڳيو نڪرندو. ڇو ته
ڪو به شخص ائين نه ٿو چئي سگهي ته جيڪي (Samples)
موضوع جي اڀياس لاءِ چونڊيا ويا آهن، اهي هر طرح
يا هر وقت انهيءَ گروهه جي نمائندگي ڪن ٿا يا جيڪي
نمونا هٿ ڪيا ويا آهن. انهن جو برابر عدد (Mean)
انهيءَ وڏي گروهه جي نمائندگي صحيح طور ڪندو، جنهن
مان نمونا نمائندگيءَ لاءِ چونڊيا ويا آهن. سمجهو
ته جيڪڏهن سڄي پاڪستان ۾ ڪڻڪ جي پئداوار 10 مڻ في
ايڪڙ لڳائي ويئي آهي، ۽ ائين چئي نٿو سگهجي ته اها
حد صحيح ايندي ۽ اهو ناممڪن آهي. ڇو ته پاڪستان جي
هر صوبي جي آبهوا ۽ زمين ۽ ٻين ڳالهين ۾ فرق آهي
جنهن ڪري هر ڪنهن صوبي جي زمين جي قوت هڪ جهڙي نٿي
رهي. انهيءَ لاءِ اهو صحيح ثابت ٿيڻ ناممڪن آهي.
پر اهو به مشڪل آهي ته پوري پاڪستان جو فصل جيڪو
تمام سٺو ٿيو آهي، اهو آخر تائين اهڙي حالت ۾ رهي
جنهن تي تخمينو لڳايو ويو آهي. ايترو ضرور ٿي سگهي
ٿو ته اڳين حالتن ۽ موجوده حالتن جي لحاظ کان ۽ هر
صوبي جي پئداوار جي صلاحيت کي ڏسندي تخمينو لڳايو
وڃي. اهو تخمينو ليڪن جي جهڪاءُ (Curve) جي لحاظ کان پورو (Normal)
هوندو آهي.
گڏيل
تعلق:
Correlation
انگن
اکرن واري تحقيق ۾ گڏيل تعلق (Correlation)
مان مراد آهي ته گڏيل تبديليون يعني ڪنهن شيءِ جي
گهٽ پئدا ٿيڻ ڪري ڪن ٻين شين تي به ساڳيو اثر پوي.
سمجهو ته جيڪڏهن ڪپهه يا ڪمند گهٽ پئدا ٿيندو ته،
انهيءَ جو اوترو اثر ڪپڙي ۽ کنڊ جي پئدائش تي
پوندو ۽ جيڪڏهن ڪپهه ۽ ڪمند وڌيڪ پيدا ٿيندا ته
ڪپڙو ۽ کنڊ وڌيڪ تيار ٿيندي يا انهن جو وڪري تي
اوترو اثر پوندو. اهڙيءَ طرح هڪڙين شين جي قدر جو
اثر ٻين شين جي قدر تي ٿيندو آهي، ته اهڙي تعلق کي
گڏيل تعلق (Correlation)
چيو وڃي ٿو. اهو اثر ڪڏهن مخالف هوندو آهي ۽ ڪڏهن
برابر هوندو آهي. يعني مخالف هن طرح هوندو آهي ته
جيڪڏهن ڪپهه ۽ ڪمند گهٽ پئدا ٿيندا ته ڪپڙو ۽ کنڊ
گهٽ تيار ٿيندي. اهو اثر برابر رهندو، پر ڪپڙي ۽
کنڊ جي گهٽتائي ڪري انهن جو قدر وڌي ويندو ۽ جنهن
ڪري سندن قيمت وڌي ويندي ۽ اهڙي حالت ۾ اهو اثر
مخالف هوندو. اهڙي طرح گڏيل تعلق ٻن قسمن جو هوندو
آهي.
|
1-برابري وارو گڏيل تعلق
2-مخالف گڏيل تعلق
3-برابر تعلق |
Postive
Correlation
Nagative
Correlation
Normal
Correlation |
(مثبت
تعلق)
(منفي تعلق) |
گڏيل
تعلق جي حسابي قيمت وڌ ۾ وڌ 1+1 ۽ گهٽ ۾ گهٽ 1-
آهي. +1 ظاهر ڪندو آهي ته تبديلين (Variables)
۾ مثبت يا گڏيل تعلق آهي. -1 ظاهر ڪندو آهي ته
تبديلين (Variables)
۾ منفي گڏيل تعلق آهي. برابر تعلق ظاهر ڪندو آهي
ته انهن ۾ ڪو تعلق نه آهي.
مثال:
ساڳئي درجي جي 5 شاگردن جدا جدا مضمونن ۾ هيٺيون
مارڪون کنيون آهن. سندن حسابن جي مارڪن کي ٻين
مضمونن جي مارڪن سان ترتيب ڏنو ويو آهي ۽ انهن کي
ليڪن جي مدد سان ماپيو ويو آهي.
|
حساب ۽ سائنس حساب ۽ سماجي
حساب ۽
اڀياس ديني تعليم |
|
الف
ب
ت
ث
ج |
90
80
75
70
65 |
80
70
60
85
50 |
))90
*80
+75
.75
65q |
q85
80.
72+
70*
60(( |
*90
F80
+75
()75
.65 |
80+
75()
60*
71F
62. |
پهرين ترتيب ۾ مثبت يا گڏيل تعلق آهي.
ٻئي
ترتيب ۾ منفي يا مخالف گڏيل تعلق آهي.
ٽئين
ترتيب ۾ گڏيل يا مخالف تعلق ظاهر نه آهي.
اهي
مارڪون هن طرح آهن.
|
حساب |
سائنس |
سماجي اڀياس |
ديني تعليم |
|
الف
ب
ت
ث
ج |
90
80
75
70
65 |
-
-
-
-
- |
70
65
60
58
50 |
-
-
-
-
- |
60
70
72
80
85 |
-
-
-
-
- |
60
71
80
75
63 |
|
|
|
|
|
|
|
|
|
مٿي
ڏنل مارڪن جي لحاظ کان هر مضمون ۾ سندن هيٺيان
نمبر ايندا.
|
حساب |
سائنس |
سماجي اڀياس |
ديني تعليم |
|
الف
ب
ت
ث
ج |
1
2
3
4
5 |
1
2
3
4
5 |
5
4
3
4
1 |
5
3
1
2
4 |
|
|
|
|
|
|
گڏيل
تعلق ۾ جيڪڏهن قدر 100+ آهي ته انهيءَ کي مثبت
گڏيل تعلق چيو ويندو ۽ جيڪڏهن قدر (Value)
O
آهي ته پوءِ بلڪل الڳ هوندو ۽ جيڪڏهن قدر (Value)
1.00 - آهي اهو منفي گڏيل تعلق هوندو.
A
الف
هن
چارٽ ۾ بلڪل مثبت گڏيل تعلق ڏيکاريو ويو آهي. هن ۾
ڏيکاريل نتيجو مشڪل سان نڪرندو آهي هتي فقط ٻن شين
جو نتيجو فرضي طور ڏنو ويو آهي. انهن ساڳي ڳڻپ کي
جيڪڏهن فهرست ۾ رکيو وڃي ته اها هن ريت ٿيندي.
مٿي
ڏنل سادو گڏيل تعلق جو چارٽ الف ۽ ب جو هڪ ٻئي ۾
تعلق ظاهر ڪري ٿو. جڏهن ته گڏيل تعلق 1.00+ آهي.
|
|
الف |
ب |
ت |
ث |
ج |
ح |
خ |
د |
ذ |
ر |
|
الف امتحان جون مارڪون |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
13 |
|
ب امتحان جون مارڪون |
4 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
14 |
15 |
فهرست نمبر
مٿي
ڏنل فهرست ۾ ڏسنداسين ته ب الف کان 2 مارڪون مٿي
آهي. عام طور تي ٿيندو ب ۽ الف +2
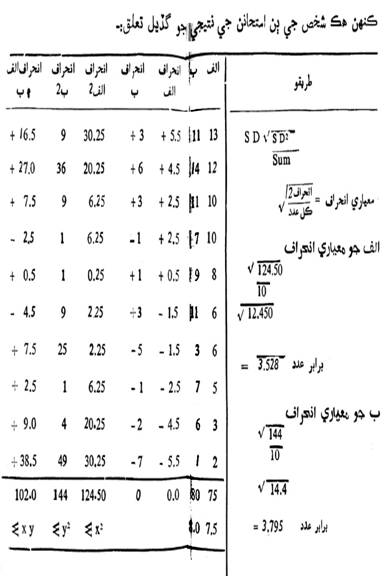
مٿيون طريقو هن ريت آهي:
(1)
الف (x)
۽ ب (y)
جي ڪل نمبر جو برابر عدد (Mean)
ڪڍو. (مٿي ڏنل فهرست ۽ طريقي ۾ ڏسندا).
(2)
الف ۽ ب جي ڪل نمبر جو معياري انحراف (,D) (الجبرا جي طريقي تي) ڪڍو.
(3)
الف ۽ ب جي معياري انحراف جو ٻيو مول (Square)
(x2 y2)
ڪڍو. انهن جو جوڙ ڪريو (x2y2∑).
(4)
الف ۽ ب (x
y)
جي ضرب ڪري سڀني عددن جو جوڙ ڪري
(∑x
y).
(5)
اُنهن سڀني عددن کي گڏ ڪرڻ کان پوءِ ڏنل طريقي تي
نتيجو ڪڍيو ويندو.
درجاتي، گڏيل تعلق معلوم ڪرڻ:
RANK ORDER
CORRELATION
انساني خصوصيتن جي پيمائش لاءِ عدد مقرر ڪري نٿا
سگهن، انهيءَ ڪري تحقيق ڪندڙ انهن جي خصوصيات کي
درجن ۾ ورهائيندا آهن. هيءُ طريقو ڪنهن جي شخصيت ۽
ڪردار کي پيمائش ڪرڻ جو آهي ۽ انهيءَ جي نشاني ”P“
هوندي آهي.
هن
جو طريقو هي آهي:
مثال:
ماڻهن جو نوڪري جي لحاظ کان درجاتي ورهاڱي ڪيو ويو
آهي ۽ انهن کي سندن ڪارڪردگي جي لحاظ کان هن ريت
درجاتي ورهاڱي ۾ رکيو ويو آهي، ۽ انهن جو درجاتي
گڏيل تعلقو معلوم ڪريو.
|
نالو |
نوڪري جو عرصو |
نوڪري جي لحاظ کان درجو |
ڪم جي لحاظ کان درجو |
فرق |
فرق2 |
|
الف
ب
ت
ث
ج
ح |
12
10
8
6
5
3 |
2
3
1
5
6
4 |
5
1
6
6
2
3 |
3
2
3
1
4
1 |
9
4
6
1
16
1 |
|
6-- |
|
|
|
|
40 |
جواب
منفي
درجاتي گڏيل تعلق 0.14 –
انو
مان جي پرک
Testing of
Hypothesis
سائنسي تحقيق ۾ انومان جي پرک وٺڻ لازمي هوندي
آهي. انومان تي گڏ ڪيل مواد جو تجزبو ڪري ۽ نتيجو
ڪڍڻ کان پوءِ اهو ڏٺو ويندو آهي ته اهو نتيجو شڪي
ته نه آهي يا ٿي سگهڻ جهڙو يا برابر آهي يا بلڪل
سوچيل انومان سان ٺهڪي اچي ٿو. يعني جيڪي ڪجهه
انومان لاءِ حقيقتون سوچيون وينديون آهن، اهي
ڪيتري قدر انومان جي نتيجي جي پٺڀرائي ڪن ٿيون
انهيءَ لاءِ انومان جي پرک ورتي ويندي آهي.
نل
انومان يا برابر عدد ۾ معنيٰ خيز فرق
Null-Hypothesis
and Significance Mean Difference
اهڙي
طرح جيڪڏهن ڪن به ٻن چونڊيل گروهن تي جدا جدا
طريقن تي تحقيق ڪئي وڃي ۽ پوءِ ٻنهي کي هڪ ئي
طريقي تي پرکيو وڃي ۽ انهيءَ ۾ فرق اچي ته انهيءَ
جا ٻه سبب ٿي سگهن ٿا:
(1)
اهو فرق مختلف طريقن تي تحقيق ڪرڻ ڪري ٿي سگهي ٿو
جنهن جو مطلب ٿيندو ته ٻئي طريقا هڪ ٻئي کان مختلف
آهن ۽ انهن گروهن سان انهن جو تعلق نه آهي يا اهي
انهن گروهن جي نمائندگي نٿا ڪن، جن مان اهي نمونا
ورتا ويا آهن.
(2)
نمونن (Sampling
Errors)
جي چونڊڻ ۾ غلطي ٿي سگهي ٿي. اهڙن سببن کي نل
انومان جي مفروضي جي شڪل ۾ بيان ڪيو وڃي ٿو. اهڙن
سببن کي نل انومان جي صورت ۾ حل ڪري سگهجي ٿو.
يعني ڪنهن به نموني جي برابر عدد ۾ فرق ۽ نمونن جي
چونڊڻ جي جيڪا غلطي هوندي آهي، انهيءَ فرق کي حل
ڪرڻ لاءِ ٻنهي نمونن يا طريقن جي برابر عددن ۽ ان
جي معياري انحرافن کي انگن اکرن جي طريقي (Statistical
Meth)
سان حل ڪيو ويندو آهي يا ظاهر ڪيو ويندو آهي.
برابر عددن (Mean)
۾ وڏو فرق آهي جو ٻنهي کي مختلف گروهن جو نمائندو
شمار ڪيو وڃي يا انومان رد ڪيو وڃي. يا انهن ۾
ڪنهن قسم جي هڪجهڙائي آهي يا انهيءَ انگن اکرن جي
نتيجي ۾ تنقيدي تناسب (Critical
Ratio)
آهي، جيڪڏهن ٻنهي نمون جو حقيقي برابر عدد (True,
Mean)
هڪ ئي هجي ته نل انومان جي مفروضي کي قبول ڪيو وڃي
ٿو. پر جي ٻنهي برابر عددن ۾ وڏو فرق آهي ته پوءِ
اهو ظاهر ٿيندو، ته اهي ٻئي گروهه مختلف آهن. اهڙي
طرح جيڪڏهن ٻنهي نمونن جي برابر عدد (True
Mean)
برابر هجن ته پوءِ انومان قبول ڪيو ويندو آهي ۽
برابر عددن جي فرق جي تنقيدي تناسب کي نموني جي
چونڊڻ جي غلطي (Error
of Sampling)
مڃيو وڃي ٿو. پر جيڪڏهن انهن جي تنقيدي تناسب ۾
فرق تمام وڌيڪ هجي ته پوءِ اهو انومان رد ڪيو
ويندو آهي. |