سمجهو ته ڪن پنجن انگن جو جوڙ 35 آهي ته 35 کي پنجن سان ونڊ ڪرڻ سان جواب نڪرندو 7. جيڪو انگن اکرن واري تحقيق ۾ برابري وارو عدد يا حسابي لحاظ کان سراسري (Average) چيو ويندو.

حسابي برابري مرڪزي جهڪاءُ جي پيماني لاءِ تمام ڪار آمد ۽ ڪارائتي هوندي آهي. هي پيماني جو طريقو مرڪزي جهڪاءُ جي لاءِ اعتبار جوڳو لکيو وڃي ٿو. انهيءَ کان سواءِ هي طريقو سادو ۽ صاف هوندو آهي ۽ ڪنهن ڳالهه جي سراسري قدر جي لاءِ بهترين طريقو آهي. 

انگريزي ۾ ٿيندو     

∑ معنيٰ عددي انگن جو جوڙ

M برابري وارو عدد (Mean)

X عدد لاءِ فرضي اکر

N عددن جو تعداد

سمجهو ته ڪل عدد هي آهن 7، 8، 5، 6، 9. جن جو برابري وارو عدد لهڻو آهي.

نوٽ :- جيڪڏهن ڪنهن شيءِ جي قدر جي برابر وارو عدد ڪڍڻو هوندو تڏهن الجبرا وانگر اکرن ۾ حساب ڪيو ويندو ۽ جيڪڏهن انگن ۾ هوندو ته پوءِ انگن ۾ جواب ڪڍيو ويندو.

گروهي مواد مان برابري وارو عدد ڪڍڻ:

Computation of Mean of Grouped Data

فهرست (9)

حسابي برابري وارو عدد 26.74 =

جاميٽري وارو برابر عدد

The Geometric Means (GM)

حسابي برابري واري عدد لاءِ عددن کي جوڙ ڪري انهن جي ڳڻپ سان ونڊ ڪيو ويندو آهي.

مثال: حسابي برابري وارو عدد                          

پر جاميٽري واري برابري واري عدد لاءِ وري عددن کي ضرب ڪري ۽ اُنهن جي ضرپ اُپت جو وري ٻيو مول ڪڍيو ويندو.

مثال ٻن عددن وارو

36  =   2 x 18

6.0  =  36   

مثال ٽن عددن وارو

2 x 6 x 3

6.0 =  36

هي طريقو آهي                    G M (x)  (x)

انگن جو ٻيو مول = جاميٽري وارو ٻيو عدد

مليل برابري وارو عدد     The Harmonic Mean (HM)

هن جو مقصد آهي ته ڪنهن قدر جو مليل برابري وارو عدد حاصل ڪيو وڃي، جيڪو هن طريقي تي ڪڍيو ويندو آهي.

HM  =      N      =     N 

هيٺين عددن جي سلسلي جو مليل برابري وارو عدد هن طريقي تي نڪرندو.  

15، 12، 12، 9، 6

مليل برابري وارو عدد (H.M) 9.8 = 

مٿين مثال کي هن طرح سمجهي سگهون ٿا. سمجهو ته 5 شاگردن جي اکرن پڙهڻ جو سراسري اندازو ڪڍڻو آهي. پنجن شاگردن جي هڪ منٽ ۾ هر هڪ جي اکرن پڙهڻ جو اندازو آهي، 6، 9، 12، 12، 15 ۽ شاگردن کي 1800 اکر پڙهڻ لاءِ آهن ۽ شاگردن کي سلسلي وار پڙهڻ لاءِ 6، 9، 12، 12 ۽ 15 منٽ کپن. ۽ اسان کي گڏيل سراسري جي رستي هڪ منٽ ۾ اُنهن اکرن جو اندازو ڪڍڻو آهي جو ٿيندو 9.8 مثال مٿي ڏسو.

مرڪزي جهڪاءُ جي پيمائش لاءِ مثالي عدد (Mode) وچون عدد (Medium) ۽ برابري وارو عدد (Mean) گهڻو استعمال آهي پر ڪن مسئلن ۾ جاميٽري وارو برابر عدد Geometric Means ۽ مليل عدد Harmonic Means کي استعمال ڪيو ويندو آهي.

مثال 1900 ۽1920 ۾ شاگردن جي داخلا 6،99،000 ۽ 24،96،000 هئ. انهيءَ ٻنهي سالن جي ڪنهن به وچ واري سال جي داخلا ڪيتري هئي انهيءَ جو اندازو اُنهن ٻنهي عددن جي مدد سان ڪڍي سگهجي ٿو. اهڙي طرح ٻنهي انگن جي سراسري ٿيندي 1597،500 . پر تخميني طور چئي سگهجي ٿو ته اها 16،00،000 هوندي ۽ اهڙي طرح سان داخلا جو واڌارو وقت جي لحاظ کان وڌندو رهيو هوندو.

پر جي ٻي مول جي مناسبت سان ڏٺو وڃي ته 1900 جي داخلا 1900 جي داخلا سان مناسبت رکي ٿي جيڪا برابر هوندي 1920 جي مناسبت سان. انهيءَ جو طريقو هي آهي.

مثال:     1910    6,96,000 x 24,96,000

1910    1324,000

جواب ٿيو 1324،000 يا 509 سيڪڙو. اهڙي طرح انهيءَ کان پوءِ جي داخلا جو به اندازو لڳائي سگهبو. يعني جيڪڏهن 1930 ۾ داخلا جو انگ ڪڍڻو هوندو ته هن طرح ڪڍي سگهبو:

24,96,000 x 0.9

اهڙي طرح ڪنهن ساڳئي قسم جي مٿي ڏيکاريل عدد حاصل ڪرڻ لاءِ جاميٽري وارو برابر عدد يا ٻيو مول ڪڍڻ گهرجي جيڪو صحيح هوندو.

ٻيو مثال :

سمجهو ته  1937 ۽ 1941ع ۾ شاگردن جي داخلا جو اندازو ڏسڻو آهي پر داخلا جا انگ اکر 1930 ۾ 6،67،000 آهن ۽ 1940 ۾ 12،28،000 آهن، ٻي ڪابه معلومات نه آهي. ڪل 10 سالن جي معلومات حاصل ٿيل آهي. انهيءَ لاءِ هي طريقو ٿيندو:

جيڪڏهن مناسبت جي لحاظ کان ڪڍنداسين ته ٿيندو:

                    1.84   

Logrithms  جي مدد سان جڏهن انهيءَ جو ٻيو مول ڪڍنداسين ته اهو نڪرندو 1.06 ۽ جيڪڏهن 1940 جي انگ 12،28،000 کي ٻيو مول 1.06 سان ضرب ڪجي ته جواب ٿيندو 129968000 ۽ اُنهن جو ٻڌن انگن ۾ جواب ٿيندو 13،00،000 ۽ اهو ئي تخميني لڳائڻ جو سٺو طريقو آهي.

ليڪن واريون تصويرون       Diagram

انگن اکرن واري تحقيق ۾ پهريائين گڏ ڪيل مواد کي مختصر ڪري ترتيب ڏنو ويندو آهي پوءِ آساني لاءِ انهن کي فهرستن ۾ رکيو وڃي ٿو. ڇو ته انگن ۾ گڏ ڪيل مواد مان نتيجو ڪڍڻ مشڪل هوندو آهي، تنهن ڪري آسانيءَ لاءِ مواد کي مختصر ڪري جدا جدا حصن ۾ ورهائي ۽ اُنهن کي فهرستن نقشن ۽ تصويرن ۾ ڏنو ويندو آهي، ته جيئن گهڻو مواد انهن تصويرن جي مدد سان هڪدم نظر ۾ اچي وڃي ۽ نتيجو صحيح نڪري اچي. انهيءَ ڪري پورو مواد جيڪو سون صفحن تي لکي سگهجي انهيءَ کي هڪ تصوير ۾ ظاهر ڪيو وڃي ٿو، جنهن ڪري تحقيق ڪندڙ ۽ پڙهندڙ جو وقت بچيو پوي. اهڙي طرح مواد کي نقشن، چارٽن، تصويرن، فهرستن ۽ ليڪن جي مدد سان هڪ هنڌ جمع ڪري نظرن ۾ آندو وڃي ٿو، جنهن مان هيٺيان فائدا ٿين ٿا:

(1)  تحقيق اثرائتي ٿئي ٿي (2) مواد مختصر ٿي اڳيان اچي ٿو (3) مواد جي ڀيٽ آسان ٿئي ٿي (4) تحقيق ڪندڙ ۽ پڙهندڙ جو وقت بچي ٿو (5) مواد هڪ نظر ۾ اڳيان اچي ٿو.

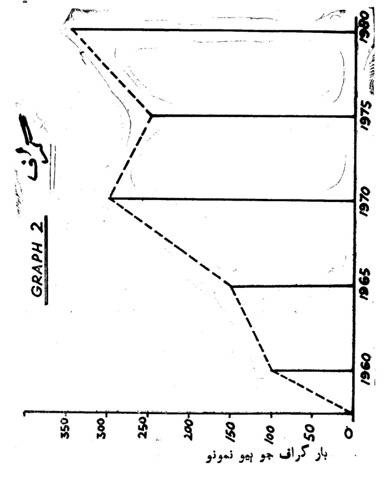
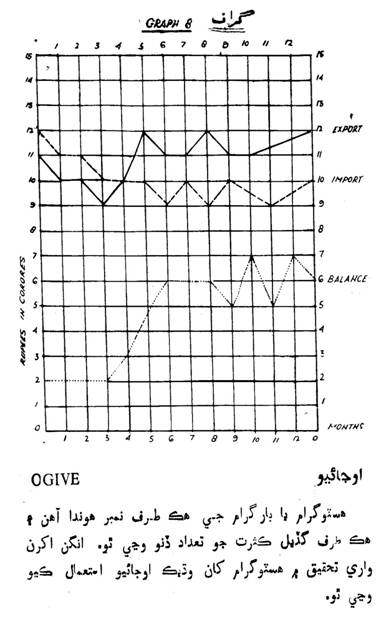
سادو بار ڊايا گرام يا هڪ طرفو ڊايا گرام

SIMPLE BAR DIAGRAM OR ONE DIMENIONAL DIAGRAM OR HISTOGRAM

انگن اکرن وارن تصويرن جا هيٺيان قسم آهن:

(1) هڪ طرفيون ليڪون:- هن ۾ سڌيون ليڪون هونديون آهن. جيڪي ڪنهن مواد جو اندازو ٻڌائينديون آهن.

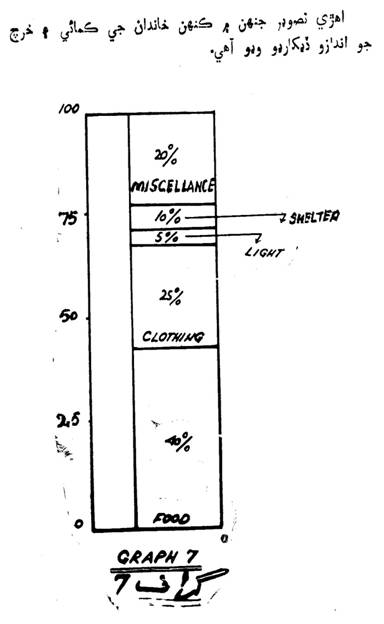
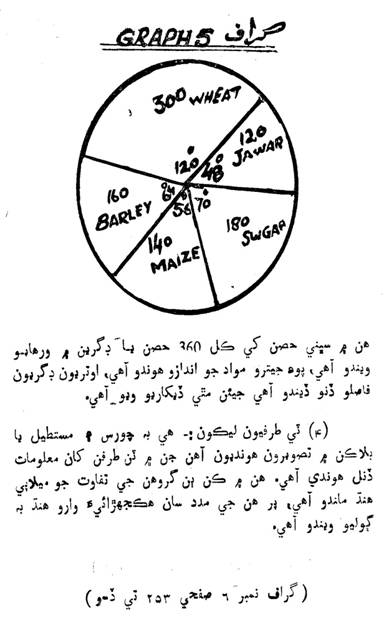
(2) ٻه طرفيون ليڪون: هن ۾ چورس يا مستطيل تصويرون هونديون آهن جن ۾ ٻن طرفن کان معلومات ڏنل هوندي آهي:

(گراف نمبر ٽيون صفحي 250 تي ڏسو)

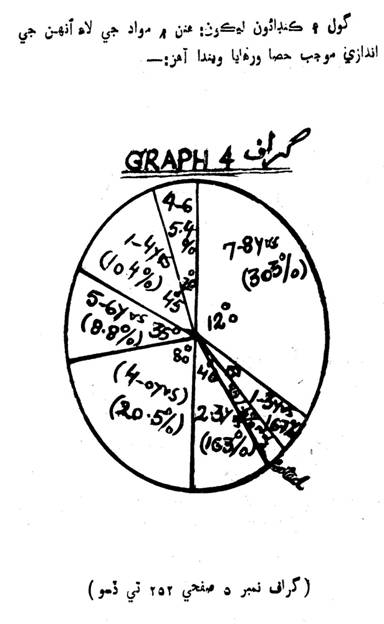
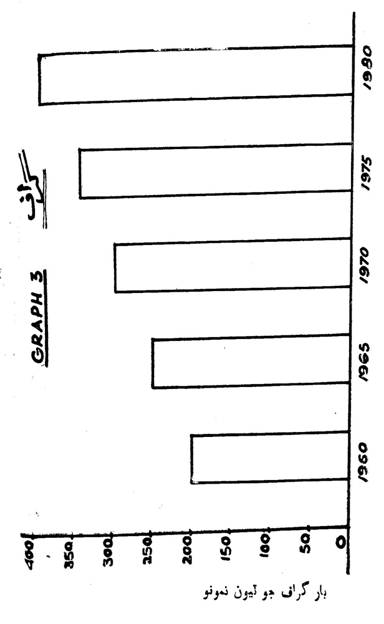
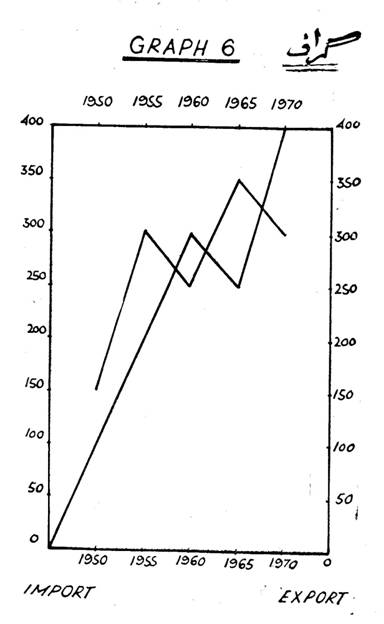
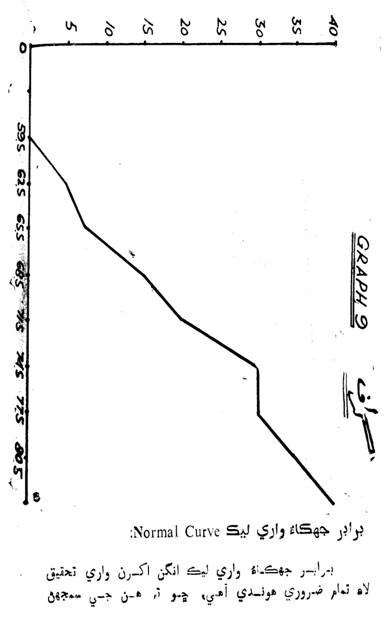
کان سواءِ انگن اکرن کي سمجهائي نه سگهبو نه وري، انومان جي حقيقي نتيجي ۽ رٿيل نتيجي کي ڀيٽي سگهبو ته نتيجو ڪيتري قدر صحيح آهي: نه وري برابري کي ڀيٽي سگهبو ۽ پيماني کي صحيح ثابت ڪري سگهبو. انهيءَ کان سواءِ ڪثرتي ورهاڱي (Frequencies)  کي به برابر جهڪاءُ واري ليڪ جي مدد سان پرکيو وڃي ٿو. اهڙي طرح برابر جهڪاءُ واري ليڪ انگن اکرن جي پيماني ڀيٽ ۽ برابري لاءِ ڪم آندي وڃي ٿي.

ڪثرتي برابر ورهاڱي لاءِ برابر جهڪاءُ واري ليڪ هن ريت استعمال ٿيندي آهي. مثال ڪثرتي برابر ورهاڱو هن ريت آهي:

(فهرست 10)

 ٻيو مثال:

سمجهو ته 40 استادن جي قابليت جو مشاهدو ڪيو ويو آهي ۽ انهن جو نتيجو هن ريت رهيو:

نئون صفحو --  ڪتاب جو ٽائيٽل صفحو
ٻيا صفحا 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

هوم پيج - - لائبريري ڪئٽلاگ